- ректору КГПУ, заведующего кафедрой геометрии и методики обучения математике, кандидату педагогических наук, профессору Юрию Александровичу Дробышеву;

- доктору педагогических наук, профессору кафедры геометрии и методики обучения математике Ирине Васильевне Дробышевой.

Отдельное спасибо научному руководителю - доктору педагогических наук, профессору Татьяне Сергеевне Поляковой.

Выражаем признательность ученому секретарю, кандидату педагогических наук, доценту Ларисе Евгеньевне Князевой, за помощь в организации процедуры защиты, а также уважаемому председателю и членам совета К. 212.206.01 за внимательное рассмотрение нашей диссертации, высказанные ценные замечания и пожелания.

Актуальность темы исследования. Характерной чертой современной образовательной ситуации являются динамичное развитие и кардинальные изменения как в структуре и содержании образования, так и в его концептуальных основах. С одной стороны, причиной этого является государственный заказ и проводимая Министерством образования и науки реформа образования, с другой – бурное развитие общепедагогических, дидактических и методических исследований. Качественные изменения в педагогических концепциях неизбежно влекут изменения в методике обучения и воспитания конкретных образовательных дисциплин. Так, теория и методика обучения математике, созданная в рамках субъектно-объектной модели педагогики советского периода, не может быть с таким же успехом применима в рамках личностно-ориентированного и развивающего обучения. Между тем методические идеи, созвучные этим педагогическим концепциям, были популярны и бурно обсуждались математической и методической общественностью еще в дореволюционной России.

Отметим, что 90-е годы ХХ в. характеризовались резкой и часто не очень обоснованной критикой тех несомненных достижений в сфере образования, которых достигла наша страна в течение ХХ в. Лишь сравнительно недавно ситуация объективизировалась, практически на всех уровнях социума вновь признается высокий уровень отечественного образования. Так, в выступлениях руководства страны, в частности, Президента РФ, признается, что исторически сложившаяся в России система образования «демонстрирует значительные преимущества перед многими зарубежными аналогами»1, причем наиболее качественной является её естественно-математическая составляющая.

В то же время в публикациях Ж.И. Алферова, В.И. Арнольда, Ю.М. Колягина, Л.Д. Кудрявцева, С.М. Никольского, Т.С. Поляковой, Н.Х. Розова, В.А. Садовничего, И.Ф. Шарыгина и мн. др. неоднократно подчеркивается, что отечественное математическое образование было и до сих пор является общепризнанным мировым эталоном.

Этот факт актуализирует необходимость исследований, посвященных истории отечественного математического образования. Какими путями оно развивалось, достигнув в середине ХХ в. эталонного уровня? Как влияла на этот процесс подготовка учителя математики? Какова роль в нем математической науки и ученых-математиков, преподавателей высших учебных заведений? Как зарождаются и развиваются методические идеи? Эти и другие глобальные проблемы, связанные с историей математического образования, несомненно актуальны для современного этапа его развития, т.к. они позволяют не только выявить факторы, способствовавшие его эффективности в ретроспективе, но и наметить перспективные направления совершенствования математического образования.

Поэтому интенсивный поиск и разработка методической составляющей современного педагогического процесса порождают спрос на исторические знания, выступающие в некоторых случаях в качестве образцов-эталонов. Для успешного использования этих эталонов они должны быть исторически отслежены и представлены в большом многообразии. В таком случае по этим эталонам можно будет создавать новые методические концепции и системы, которые будут решать новые задачи в новой социально-педагогической ситуации. Все это обусловливает тот факт, что в изучение отдельных аспектов истории отечественного математического образования включается все более широкий круг исследователей.

За последние годы появились серьезные монографические исследования общей истории математического образования в России (Ю.М. Колягин, Т.С. Полякова); обширные статьи по отдельным её направлениям в специализированной периодике (Р.З. Гушель, С.С. Демидов, Ю.А. Дробышев, Т.С. Полякова, Н.Х. Розов, О.А. Саввина, В.М. Тихомиров, Р.С. Черкасов и мн.др.); защищаются кандидатские (Г.И. Алексеева) и докторские (О.А. Саввина) диссертации; по этой проблематике проводятся юбилейные научные конференции.

Достаточно красноречив тот факт, что из 38 опубликованных докладов российской презентации на Х Международном конгрессе по математическому образованию (Копенгаген, 2004) 14 полностью или частично посвящены истории отечественного математического образования.

Особое внимание исследователей и широкой математической общественности обращено в последние годы на персоналистический компонент истории математического образования в России. Научно-методические конференции ведущих вузов очень часто посвящены памяти выдающихся математиков, внесших значительный вклад в развитие математического образования нашей страны. Так, только за последние несколько лет состоялись конференции, посвященные научной и методико-педагогической деятельности М.В. Остроградского (С.-Петербург, Калуга, 2002), А.П. Киселева (Орел, 2003), Л.Ф. Магницкого (Тверь, 2003), А.Н. Колмогорова (Москва, Ярославль, 2003), И.К. Андронова (Москва, 2004), А.И. Хинчина (Калуга, 2004) и др. По материалам конференций публикуются сборники статей и тезисов, которые содержат новые сведения о творческой биографии, педагогических и методических воззрениях выдающихся деятелей математического образования и характеризуют развитие генерированных ими методических идей.

Историко-биографические книги часто характеризуют роль выдающегося математика в развитии отечественного математического образования. Так, например, в книге о А.Н. Колмогорове имеется специальный раздел «Колмогоров и математическое образование».

Однако в публикациях подобного рода мы не встречали профессионального анализа методического наследия выдающихся математиков, в то время как со времен Л.Эйлера (см. исследования Т.С. Поляковой) методическое творчество явно или неявно очень часто занимает значительное место в их деятельности.

Это целиком и полностью относится к методическому наследию выдающегося мыслителя и математика ХХ в., педагога и методиста Д.Д. Мордухай-Болтовского (1876-1952).

Наиболее полно и систематизированно педагогические и методические воззрения Д.Д. Мордухай-Болтовского представлены в написанных им отчетах о работе I и II Всероссийских съездов преподавателей математики (1912, 1915), в ряде научных публикаций в центральных педагогических и методических журналах, а также в оставшихся неопубликованными материалах.

С именем Д.Д. Мордухай-Болтовского мы связываем не только развитие теоретической методики обучения математике первой половины XX в., но и становление общего среднего и особенно высшего математического образования на Дону.

Д.Д.Мордухай-Болтовской разрабатывал наиболее актуальные для своего времени проблемы математического образования среднего и высшего уровней: теоретико-методологические основы школьного курса математики, содержание математического образования, формы и методы обучения математике, теория и методика урока математики, вопросы подготовки учителей математики и организации методической аспирантуры и др. Его перу принадлежат многочисленные труды по истории и философии математики и даже по истории развития в математическом образовании некоторых методических идей.

Следует признать, что значительный вклад Д.Д. Мордухай-Болтовского в различные отрасли науки не был оценен по достоинству, несмотря на очень большой авторитет, который он имел в педагогико-математическом сообществе, значительное количество учеников и последователей.

Тем не менее, его жизни и педагогической деятельности (преимущественно в высшей школе) посвящены статьи ученых Дона: М.Б. Налбандян, Ю.С. Налбандян, Н.М. Несторовича, М.Г. Хапланова, М.П. Черняева и др.

В 90-х гг. ХХ в. интерес к личности и научному наследию Д.Д. Мордухай-Болтовского заметно возрастает. Целый ряд исследователей публикует работы, посвященные изучению наследия ученого. В 1993 г. в исторических очерках «Деятели русской науки XIX-ХХ вв.» (СПб., ИИЕТ. Вып.II) выходит статья А.С. Степановой «Неизвестные страницы жизни и научной деятельности Д.Д. Мордухай-Болтовского (1876-1952)». В 1994 и 1998 годах появляются депонированные работы М.Б. Налбандян и Ю.С. Налбандян, освещающие некоторые аспекты научно-педагогической деятельности Д.Д. Мордухай-Болтовского в Варшаве и Ростове-на-Дону. Наконец, в 1998 г. в серии «Философы России ХХ века» выходит собрание сочинений Д.Д. Мордухай-Болтовского, объединенных триадой «философия-психология-математика». Составитель сборника А.В. Родин предваряет собрание сочинений краткими биографическими сведениями об ученом и предпринимает попытку характеристики его научного наследия. Тем не менее, полное представление о творческой биографии Д.Д. Мордухай-Болтовского, научном и – особенно – методическом его наследии до сих пор отсутствует.

Возникает противоречие между значительным интересом научного сообщества к творческой биографии и научному наследию Д.Д. Мордухай-Болтовского и практической невозможностью удовлетворения этого интереса вследствие отсутствия профессионального анализа научного и педагогического творчества этого выдающегося ученого.

Мы считаем, что существенный вклад в разрешение методической компоненты этого противоречия внесет решение основной проблемы нашего исследования: анализ и оценка вклада Д.Д. Мордухай-Болтовского в развитие теории и методики математического образования, исследование эффективности его методических идей в современной практике обучения математике.

Итак, возможность разрешения сформулированного нами выше противоречия, а также потенциальная осуществимость использования при построении современных методических систем наследия Д.Д. Мордухай-Болтовского в качестве историко-методического образца-эталона обусловливает актуальность заявленной нами темы исследования.

Методологический аппарат исследования.

Объект исследования– отечественная теория и методика математического образования ХХ в. в их историческом развитии.

Предмет исследования –творческая биография, научно-педагогическая деятельность и методическое наследие Д.Д. Мордухай-Болтовского как выдающегося деятеля отечественного математического образования ХХ в.

Цель исследования– создание творческой биографии Д.Д. Мордухай-Болтовского; поиск и научный анализ работ, составляющих методическое наследие ученого, выявление возможностей его использования в современном математическом образовании.

Гипотеза исследования формулируется нами к той его части, которая касается реализации методических идей Д.Д. Мордухай-Болтовского, следующим образом: реализация методических идей Д.Д. Мордухай-Болтовского будет эффективной в том случае, если:

· они органично встраиваются в современные психолого-педагогические и методические концепции математического образования;

· математическая компонента этих идей не утратила своей актуальности и реализует многообразные и современные функции математического образования;

· в процессе их реализации используются современные технологии обучения математике;

· на их основе может быть построена современная методическая система, цели которой не противоречат целям современного математического образования.

Цель, предмет, и гипотеза исследования определили ведущие его задачи:

1.Восполнить недостающие фрагменты творческой биографии Д.Д. Мордухай-Болтовского, документально обосновать некоторые известные её факты.

2.Ввести в научный оборот архивные документы, малоизвестные публикации и неопубликованные материалы, касающиеся жизни, деятельности и творческого наследия Д.Д. Мордухай-Болтовского.

3.Отобрать и проанализировать те проблемы методического наследия Д.Д. Мордухай-Болтовского, которые остаются актуальными для современного отечественного математического образования.

4.Разработать теоретико-методические основы элективного курса «Двойственные преобразования», развивающего идею Д.Д. Мордухай-Болтовского о построении школьного курса геометрии на основе принципа двойственности.

5.Проанализировать опыт изучения курса «Двойственные преобразования» в рамках профильного обучения математике на старшей ступени общего образования.

Методологические и теоретические основы исследования составляют:
- работы по методологии исторического, историко-педагогического и историко-методического исследования (Н.А. Бердяев, П.В. Горностаев, Р.З. Гушель, Г.М. Иванов, А.М. Коршунов, Ю.В. Петров, Ю.П. Истратов, Н.И. Кузнецова, С.Р. Микулинский, Н.И. Родный, Н.В. Метельский, В.Н. Мощанский, Н.В. Назаров, З.И. Равкин, К. Ясперс и др.);

- фундаментальные труды по истории математики и математического образования (И.К. Андронов, И.Г. Башмакова, С.Е. Белозеров, А.Н. Боголюбов, М.Я. Выгодский, Б.В. Гнеденко, С.С. Демидов, Ю.А. Дробышев, В.А. Добровольский, Ю.М. Колягин, А.В. Ланков, Г.П. Матвиевская, Ф.А. Медведев, Н.В. Метельский,  М.Б. Налбандян, Ю.С. Налбандян, Т.С. Полякова, В.Е. Прудников, Р.С. Черкасов, И.З. Штокало, А.П. Юшкевич и др.);

- исследования, посвященные интеллектуальной истории Дона, косвенно используемые нами при воссоздании ростовского периода творческой деятельности Д.Д. Мордухай-Болтовского (С.Е. Белозеров, И.М. Гегузин, Я.М. Ерусалимский, Ю.Ф. Коробейник, Н.А. Решетова, З.Н. Римская, Н.Н. Рожанская, Р.М. Ситько, Ю. Фельштинский, М.Г. Хапланов и др.);

- работы, освещающие актуальные проблемы школьного математического образования (Ж.И. Алферов, В.И. Арнольд, Х.Ж. Ганеев, Б.В. Гнеденко, Я.И. Груденов, В.А. Гусев, Г.В. Дорофеев, А.В. Дорофеева, Ю.А. Дробышев, И.В. Дробышева, О.Б. Епишева, Т.А. Иванова, Л.Д. Кудрявцев, А.Е. Малых, А.Г. Мордкович, С.М. Никольский, Т.С. Полякова, С.И. Попов, Н.Х. Розов, В.А. Садовничий, Г.И. Саранцев, А.Т. Умарова, Т.Т. Фискович, А.Н. Чалов, О.В. Шабашова, И.Ф. Шарыгин, А.И. Щетников, П.М. Эрдниев, И.С. Якиманская, А.В. Ястребов и др.);

- теоретические разработки ведущих концепций современного образования, в том числе математического, в той или иной мере используемые нами при разработке теоретико-методических основ курса «Двойственные преобразования» (Е.В. Бондаревская, Н.Я. Виленкин, С.П. Грушевский, В.А. Гусев, В.В. Давыдов, Г.В. Дорофеев, Л.В. Занков, Т.А. Иванова, М.И. Кларин, Г.Л. Луканкин, В.В. Орлов, В.В. Попков, Г.К. Селевко, В.В. Сериков, Л.М. Фридман, А.В. Хуторский, Д.Б. Эльконин и др.);

- работы, в которых рассматриваются приложения принципа двойственности (в частности, к геометрии), использованные нами при разработке содержательных основ курса «Двойственные преобразования» (С.Л. Грейтцер, Г.С. М. Коксетер, Т.В. Малкова, В.М. Монахов, М.П. Пистрак, В.В. Попков, Б.Н. Саморуков, Т.Т. Фискович, М.П. Черняев, И.М. Яглом и др.).

Для реализации поставленных цели и задач в работе использовались научно-теоретические, эмпирические и статистические методы исследования. При проведении исторической части исследования (гл.1) мы использовали: изучение архивных документов и первоисточников (воспоминания, эпистолярное наследие, рукописи); аналитико-синтетический метод изучения фактов в единстве с историческим подходом к изучаемым явлениям; сравнительно-исторический метод; метод моделирования и воссоздания исторического образа; метод беседы, интервьюирования; методы обобщения и систематизации полученного материала и др.

При создании историко-методической части работы (гл.2) были применены следующие методы: историко-научный и методический анализ оригинальных текстов опубликованных методических работ Д.Д. Мордухай-Болтовского и рукописей ученого, в которых рассматривались методические проблемы обучения математике; теоретический метод анализа и обобщения источников, отражающий развитие методической теории обучения математике; сочетание ретроспективы с перспективой при выявлении возможностей использования методического наследия ученого в современном математическом образовании; методы классификации и содержательного обобщения и др.

В разработке опытно-экспериментальной части исследования (гл.3) основными методами явились:
1) экспериментальные методы (элементы констатирующего и формирующего экспериментов);
2) диагностические методы (опрос, тестирование, беседа, метод самооценки и т.п.);
3) метод сравнительного сопоставления количественных данных;
4) методы статистического анализа.
Высчитаны процентные соотношения, индексы и коэффициенты; полученные результаты обобщены в таблицы, даны их графические интерпретации в виде диаграмм, графиков, гистограмм.

Источниковедческую базу исторической части исследования прежде всего составляют архивные материалы, предоставленные нам:

а) крупнейшими архивами страны:
1)Российским государственным историческим архивом (РГИА, фонды: 733, 740);
2)Центральным государственным историческим архивом г. Санкт-Петербурга (ЦГИА СПб, фонды: 14, 114);
3)Петербургским филиалом архива Российской Академии Наук (ПФА РАН, фонды: 162, 821, 967);
4)Государственным архивом Ростовской области (ГАРО, фонды: 42, Р-46, Р-67, Р-97, 527, Р-1019, Р-1452, 1727, Р-2605);

б) архивами учебных заведений г. Ростова-на-Дону (РГУ, РГПУ, РГУПС);

в) семейным архивом Д.Д. Мордухай-Болтовского.

В качестве источников исторической и методической части исследования кроме опубликованных материалов использовались: рукописи методических статей Д.Д. Мордухай-Болтовского; публицистика Д.Д. Мордухай-Болтовского 1917-1918 гг.; деловая переписка ученого 1902-1952 гг.

Опытно-экспериментальной базой практической части исследования явился физико-математический лицей №33 г.Ростова-на-Дону. Экспериментальная работа проводилась в условиях естественного учебного процесса (8-10 классы) при изучении курса геометрии и чтении элективного курса «Двойственные преобразования».

Исследование проводилось в три этапа: Первый этап (1999-2001 гг.) был посвящен разработке общей концепции исследования на основе анализа педагогической, психологической и методической литературы; проведено обоснование проблемы исследования, изучен уровень её разработанности в науке. Осуществлялся поиск печатных и архивных материалов о научно-педагогической деятельности, творческой биографии и методическом наследии Д.Д. Мордухай-Болтовского.

На втором этапе (2001-2003 гг.) осуществлено углубленное изучение документальных источников, сделан сравнительно-сопоставительный анализ полученных из различных источников данных, определены и изучены те проблемы теории и методики обучения математики (с акцентом на геометрию), которые содержатся в методическом наследии Д.Д. Мордухай-Болтовского и не потеряли своей актуальности. Сформулирована рабочая гипотеза. Начата опытно-поисковая работа по определению возможностей использования методических идей Д.Д. Мордухай-Болтовского в современном математическом образовании.

Третий, завершающий этап (2003-2004 гг.). Разработка теоретико-методических основ элективного курса «Двойственные преобразования», реализующего одну из конструктивных методических идей Д.Д. Мордухай-Болтовского. Осмысление и корректировка его методического аппарата и содержательной компоненты, внедрение в процесс обучения учащихся физико-математического лицея №33 г. Ростова-на-Дону в качестве элективного. Разработка методик диагностики результативности методических идей курса, сбор экспериментальных данных и их обработка, проверка эффективности. Систематизация, теоретическое обоснование и оформление результатов исследования в виде кандидатской диссертации.

Апробация и внедрение результатов исследования. Результаты исследования докладывались и получили одобрение на научных конференциях, семинарах, совещаниях: Всероссийской школе-семинаре «Профессионализация предметной подготовки учителя математики в педагогическом вузе (концепции, стандарты, программы, учебники)» (г. Ярославль, 2000); научной конференции ИИЕТ РАН «Петербургская математическая школа в период реформ XIX века», посвященной 200-летию со дня рождения М.В. Остроградского (г. С.-Петербург, 2001); XXI Всероссийском семинаре преподавателей математики (г. С.-Петербург, 2002); научно-практической конференции Ростовского областного музея краеведения (г. Ростов-на-Дону, 2004).

Внедрение научных результатов осуществлялось в процессе публикаций статей, научно-методических материалов, путем организации опытно-экспериментальной работы в лицее №33 г. Ростова-на-Дону, а также в ходе участия автора в конкурсе «Учитель года 2003». Результаты исследования внедрены в практику работы Ростовского областного ИПК и ПРО, использовались диссертантом и членами кафедры геометрии и методики обучения математики РГПУ на лекциях и семинарских занятиях в курсах истории математики и истории отечественного школьного математического образования.

По результатам исследования опубликовано 12 работ общим объемом 4,05 п.л., из них в центральной печати 4. Среди них 5 статей [5, 7, 8, 10, 12], 5 тезисов [1, 2, 3, 4, 6] и 2 методические разработки [9, 11].

Научная новизна и теоретическая значимость исследования состоят в том, что:

– в научный оборот введены новые архивные и другие ранее не опубликованные материалы, характеризующие творческую биографию и методическое наследие Д.Д. Мордухай-Болтовского, в том числе рукописи методических статей, ранее известные только «со списков», публицистика, деловая переписка;

– уточнены биографические сведения о Д.Д. Мордухай-Болтовском, в частности, документально воспроизведены последние годы жизни; представлена и приведена в систему творческая биография ученого с включением новой информации;

– методическое наследие Д.Д. Мордухай-Болтовского впервые явилось предметом целостного исследования: дана полная характеристика теоретической и практической деятельности ученого по проблемам математического образования в средней школе; особое внимание уделено анализу  проблем методики обучения геометрии, не потерявших своего значения;

– обобщенны концептуальные взгляды Д.Д. Мордухай-Болтовского на теорию и методику обучения математике в средней школе, которые расширяют представления о методических приоритетах первой половины XX в.;

– разработаны методическая система и содержательные основы элективного курса «Двойственные преобразования» для профильной школы, реализующего одну из конструктивных методических идей Д.Д. Мордухай-Болтовского; показана эффективность его реализации в современной профильной школе.

Практическая значимость исследования заключается в том, что выделенные нами методические идеи Д.Д. Мордухай-Болтовского могут выступать в качестве эталонов-образцов для моделирования методических систем в современной школе. Элективный курс «Двойственные преобразования» может быть продуктивно использован в профильном обучении математике.

Результаты и выводы исследования могут служить основой для новых работ по истории математического образования. Фактологический материал и обобщенные в диссертации положения могут входить в фундаментальные исследования и учебные пособия по истории математического образования советского периода, в реализации персонифицированного подхода к проблемам истории математического образования.

Создан сайт www.pyrkovve.narod.ru, посвященный Д.Д. Мордухай-Болтовскому, содержащий помимо основных результатов исследования использованные при написании диссертации материалы (фото, архивные документы, работы Д.Д. Мордухай-Болтовского и мн. др.)

Достоверность и обоснованность полученных научных результатов. Достоверность теоретического компонента исследования обеспечена широкой источниковедческой базой исследования, подтверждается по критерию практической проверки, по критерию непротиворечивости логики исследования, по критерию контекстуальной достоверности. Истинность практического компонента исследования обеспечена позитивными результатами его внедрения в практику работы физико-математического лицея №33 г.Ростова-на-Дону, положительной его оценкой со стороны учителей математики; применением статистических методов при обработке данных.

Положения, выносимые на защиту:

1. В диссертации предложена достаточно целостная, приведенная в систему, дополненная новыми фактами и документально уточненная творческая биография Д.Д. Мордухай-Болтовского.

2. Представленное и проанализированное в диссертации методическое наследие Д.Д. Мордухай-Болтовского вносит существенный вклад в развитие теории и методики обучения математике и должно занять достойное место в истории отечественного математического образования.

3. Многие разработанные Д.Д. Мордухай-Болтовским методико-математические проблемы не потеряли своей актуальности и могут служить эталоном-образцом для создания современных методических систем школьного математического образования.

4. Представленный в диссертации элективный курс «Двойственные преобразования» реализует одну из продуктивных идей Д.Д. Мордухай-Болтовского о построении школьного курса геометрии, основан на базе современных концепций математического образования и может быть эффективно использован в современном профильном обучении математике.

5. Выполненное исследование и практическая деятельность автора (атрибутация захоронения, создание музейной экспозиции в РГПУ, организация установки мемориальной доски по одному из адресов педагогической деятельности ученого и др.) служат объективизации истории математического образования в России и на Дону, выполняют функции научной и практической реабилитации некоторых фрагментов жизни, творческой деятельности и научного наследия Д.Д. Мордухай-Болтовского.

Структура диссертации. Диссертация состоит из введения, трех глав, заключения, списка литературы и четырех приложений. Общий объем диссертации составляет 358 страниц. Из них: 230 с. – основной текст, 16 с. – список литературы из 265 наименований. В тексте содержится 4 схемы, 10 таблиц и 3 диаграммы.

В приложении представлены:
1) архивные документы и фотоматериалы к творческой биографии Д.Д. Мордухай-Болтовского;
2) библиография работ Д.Д. Мордухай-Болтовского, содержание архивного фонда Д.Д. Мордухай-Болтовского (ПФА РАН ф.821, оп.1);
3) программа и дидактические материалы к занятиям элективного курса «Двойственные преобразования»;
4) инструментарий опытно-экспериментальной работы.

ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ

Во введении формулируется проблема исследования, обосновывается его актуальность, определяются цель, объект и предмет, формулируются гипотеза и задачи, характеризуются методологические и теоретические основы и методы исследования. Характеризуется источниковедческая база исторической части исследования. Описываются этапы его проведения. Раскрывается научная новизна, теоретическая и практическая значимость исследования, обосновывается достоверность полученных результатов, формулируются положения, выносимые на защиту.

В первой главе «К творческой биографии Д.Д. Мордухай-Болтовского», носящей исторический характер, инициировано создание целостной, приведенной в систему, дополненной новыми фактами и документально уточненной творческой биографии ученого. Выявлены периоды творческой биографии Д.Д. Мордухай-Болтовского, к которым отнесены: 1) сведения о родословной, детских и юношеских годах (до 1898 г); 2) варшавский период (1898-1915 гг.); 3) ростовский период (1915-1947 гг.); 4) последние годы жизни (1947-1952 гг.).

В 1.1. проведен анализ публикаций, содержащих сведения о Д.Д. Мордухай-Болтовском, которые представлены: 1) изданиями, содержащими сведения справочного характера; 2) статьями, посвященными анализу научных работ Д.Д. Мордухай-Болтовского; 3)работами, в которых анализируется его методическое наследие; 4) публикациями, отражающими творческую биографию ученого и его педагогическую деятельность; 5) художественной литературой; 6) ресурсами Internet.

В процессе анализа сведений о родословной, детских и юношеских годах ученого (1.2) нами:
– обнаружены и введены в научный оборот ранее неизвестные документы, касающиеся генеалогии рода Мордухай-Болтовских, хранящиеся как в государственных архивах (РГИА, ЦГИА СПб, ПФА РАН, ГАРО), так и в частном архиве Болтовских. Благодаря этому мы смогли гипотетически восстановить генеалогию рода Болтовских, начиная с 1200 г.;
– введены в научный оборот сохранившиеся в семейном архиве Болтовских письма и воспоминания Д.Д. Мордухай-Болтовского, содержащие сведения о детских и юношеских годах. В результате этого установлены сведения о семейном укладе Болтовских, о среде, в которой он воспитывался и вырос, что оказало влияние на формирование его интересов и взглядов;
– уточнены сведения о связи Д.Д. Мордухай-Болтовского с общественным и политическим деятелем М.И. Калининым, которая лишь упоминается в работах предыдущих исследователей (Налбандян М.Б., Родина А.В., Степановой А.С.);
– обнаруженное нами в ЦГИА СПб «Дело» гимназиста 1-й классической гимназии С.-Петербурга Д.Д. Мордухай-Болтовского позволило установить проявление у Д.Д. Мордухай-Болтовского способностей и интереса к математике со школьной скамьи, что подтверждают как успеваемость по данному предмету, так и характеристики, данные его преподавателями;
– из материалов ЦГИА СПб и ПФА РАН, содержащих «Дело» студента Д.Д. Мордухай-Болтовского, нами уточнены сведения об обучении его в С.-Петербургском университете, касающиеся преподавательского состава, отношения к науке и учебе, формирования научных интересов.

В процессе исследования варшавского периода творческой деятельности Д.Д. Мордухай-Болтовского (1.3) нами:
– проанализированы и введены в научный оборот документы, касающиеся научной деятельности, карьерного роста и личной жизни ученого, хранящиеся в РГИА, ЦГИА СПб, ПФА РАН, ГАРО и в архивах учебных заведений (РГУ, РГУПС), в которых он работал;
– впервые подробно охарактеризованы деятельность Д.Д. Мордухай-Болтовского в Донском Политехническом институте (1907-1909 гг.) и материалы, касающиеся защиты докторской диссертации;
– уточнены и документально подтверждены сведения, освещающие путь Д.Д. Мордухай-Болтовского от ассистента до профессора кафедры чистой математики Варшавского Императорского университета.

В результате исследования ростовского периода творческой деятельности Д.Д. Мордухай-Болтовского нами обнаружены и  введены в научный оборот ранее не использованные документы из центральных архивов ГАРО, ПФА РАН и архивов учебных заведений РГУПС и РГУ, из семейного архива Болтовских и воспоминания учеников и сослуживцев Д.Д. Мордухай-Болтовского. Используя их, мы восполнили пробелы предыдущих исследователей жизни и творчества ученого.

Анализ творческой деятельности Д.Д. Мордухай-Болтовского позволяет утверждать, что Д.Д. Мордухай-Болтовской является не только основателем первой научной математической школы на Дону, но и организатором высшего математического образования (1.3.3). Именно он возглавлял математические кафедры при создании Донского Политехнического института в Новочеркасске (1907-1909 гг.), а затем и Донского (Северо-Кавказского, Ростовского) университета (1915-1947 гг.). Его педагогическая деятельность распространялась и на другие вузы региона (РГУПС, 1923 г.; РГПУ, 1931-1942 гг.), средние профессиональные заведения и даже общеобразовательные школы.

Им создана научная методическая школа, влияние которой через его учеников распространилось по всему Северному Кавказу. Многие из научных и методических идей Д.Д. Мордухай-Болтовского находят свое развитие в трудах современных представителей этой школы, обсуждаются на научных и методических семинарах в РГУ и РГПУ.

В первой главе нами также рассмотрена ранее неизвестная публицистическая деятельность ученого 1917-1918 гг. (1.3.4). Проведен анализ 12 статей, содержание которых позволило выявить основные черты мировоззрения ученого, его политические пристрастия и нравственные императивы, характеризующие его как представителя российской интеллигенции начала ХХ в. [10].

Результаты данной части исследования позволили уточнить и значительно обогатить биографические сведения об ученом, придать им целостность и завершенность.

При проведении исторической части исследования были использованы: а) более трехсот документов из шести различных архивов страны; б) записанные нами воспоминания учеников и коллег Д.Д. Мордухай-Болтовского; в) беседы с родственниками и материалы семейного архива Болтовских; г) публикации в местной периодической печати, освещающие педагогическую и публицистическую деятельность Д.Д. Мордухай-Болтовского; д) работы предыдущих исследователей жизни и научного творчества ученого.

Во второй главе «Актуальные проблемы школьного математического образования в методическом наследии Д.Д. Мордухай-Болтовского» нами проанализированы методические работы Д.Д. Мордухай-Болтовского.

В 2.1 выделены и охарактеризованы следующие группы материальных источников, составляющих методическое наследие ученого: 1) методические статьи, опубликованные в отечественных журналах; 2) публикации методического характера в иностранных журналах; 3) статьи по теории и методике математического образования, сохранившиеся в рукописном наследии ученого; 4) учебные пособия и курсы лекций Д.Д. Мордухай-Болтовского [3, 4]; 5)доклады организованного Д.Д. Мордухай-Болтовским методического коллоквиума.

В 2.2 выявлены и проанализированы исследования ученого по актуальным вопросам теории и методики школьного математического образования, а именно:
– методические проблемы использования эвристического метода в обучении математике (2.2.1): о сущности и правильном понимании эвристического метода; об эффективности и необходимости учета особенностей процесса коллективного познания при его использовании в объяснении нового материала; о личностно-ориентированной его направленности; о наиболее распространенных ошибках при использовании эвристического метода в обучении математике и др.
– проблемы теории и методики историзации школьного математического образования (2.2.2): о роли и функциях, различных формах и средствах, а также уровнях историзации обучения математики; о необходимости включения элементов истории математики в качестве обязательного материала для изучения в средней школе; о роли школьного учебника математики в историзации математического образования; о необходимости разнообразия литературы для дополнительного чтения, содержащей сведения историко-математической направленности; о недостатке общей исторической подготовки учителей математики и др.

Представлены предложенные Д.Д. Мордухай-Болтовским варианты решения избранных проблем методики обучения геометрии в школе, среди которых:
– проблемы логики построения школьного курса геометрии (2.3.1): об учете «психологии» его построения, под которой он понимал ожидаемость дальнейшего содержания курса, обеспечивающую психологическую готовность к его восприятию; о достоинствах и недостатках различных приемов построения учебного курса; о роли и месте аналогии; о возможности применения принципа двойственности и др.;
– методические проблемы школьного геометрического доказательства (2.3.2): об особой роли первых доказательств школьной геометрии; необходимости избегать доминирования формально-логических приемов доказательства первых теорем, в т.ч. метода «от противного»; о значительном потенциале развития логического мышления средствами геометрических доказательств; об особой роли моделей в школьном геометрическом доказательстве; об эффективности одновременного использования как интуитивного, так и логического компонентов доказательства; о соотношении анализа и синтеза в геометрическом доказательстве и их методических преимуществах; о возможностях использования эвристик на различных этапах доказательства и др.;
- проблемы использования геометрических моделей и развития пространственного воображения учащихся (2.3.3): о «логике и психологии» чертежа и модели; о роли и месте стереометрических моделей в школьном курсе геометрии и целях их применения; о рациональной методике использования моделей; о классификации геометрических моделей по уровню их функциональности; о методике развития пространственного воображения и «геометрической памяти»; о роли средств, создающих «стереометрическую иллюзию» в развитии воображения и др.;
- методические проблемы использования принципа двойственности в качестве основного принципа построения школьного курса геометрии (2.3.4).

В заключение этой главы показаны актуальность и ценность методического наследия Д.Д. Мордухай-Болтовского, оценен его вклад в развитие теории и методики отечественного математического образования [7].

В третьей главе «Курс «Двойственные преобразования» как пример реализации методических идей Д.Д. Мордухай-Болтовского в современном школьном математическом образовании», разработаны теоретические и методические основы этого курса, развивающего идею Д.Д. Мордухай-Болтовского о построении школьной геометрии на основе принципа двойственности; описаны педагогический эксперимент и результаты его внедрения [1, 2, 8, 9, 11].

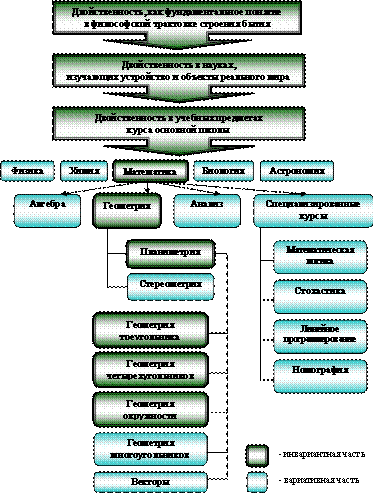
Принцип двойственности возведен в ранг методического принципа, позволяющего структурировать содержание школьного курса геометрии и реализующего основные идеи эвристического, развивающего и личностно-ориентированного обучения математике.

В 3.1 обобщен, систематизирован и проанализирован имеющийся опыт использования принципа двойственности, показавший целесообразность ознакомления учащихся средней школы с этим принципом в рамках элективного метапредметного курса «Двойственные преобразования в профильных математических школах и классах.

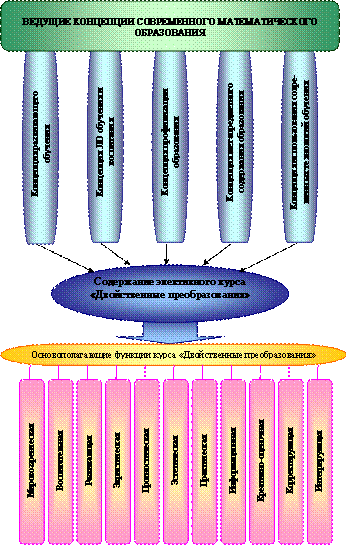
В 3.2 разработаны концептуальные и содержательные основы курса, охарактеризованы реализуемые им функции, обобщенно представленные в схеме1. Соотношение инвариантной и вариативной частей курса «Двойственные преобразования», представлено в схеме 2.

Основными принципами отбора содержания курса являются:

1.Принцип преемственности содержания с имеющейся математической подготовкой учащихся.

2.Принцип специальной направленности прежде всего на профильную математическую подготовку.

3.Принцип фундаментальности и усиления методологической составляющей содержания.

4.Принцип вариативности при сохранении инвариантного теоретического ядра.

5.Принцип минимизации, заключающийся в том, что инвариантная часть курса должна содержать необходимый минимум информации.

6.Принцип значимости персоналистического компонента, который обусловлен определяющей ролью персоналий в развитии любой теории.

7.Принцип функциональной полноты компонентов содержания, предполагающий представление в нем всех его базовых компонент.

8.Принцип соответствиясовременному уровню развития методической и педагогической науки.

При разработке программы курса с учетом указанных принципов были выделены такие разделы как «Принцип двойственности в элементарной геометрии», «Конструктивное определение двойственных преобразований», «Взаимные теоремы школьного курса геометрии», «Использование двойственных преобразований в решении задач», «Использование двойственных преобразований для конструирования теорем».

В качестве ведущих технологий обучения использовались:
1) проблемно-исследовательские технологии обучения;
2) технология проектного обучения;
3) технология эвристического «погружения»;
4) технологии индивидуализированного обучения;
5) технология организации творческих мастерских;
6) информационные и компьютерные технологии.

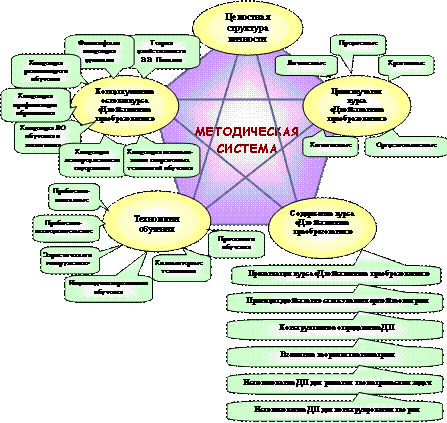
В 3.2.2 разработана методическая система курса «Двойственные преобразования» (схема 3); сформулированы и охарактеризованы основные цели его изучения.

В 3.3 и 3.4 раскрыта организация опытно-экспериментальной работы по внедрению курса «Двойственные преобразования» в учебный процесс физико-математического лицея №33 г.Ростова-на-Дону и оценка его эффективности. Эксперимент состоял из двух этапов: поисково-констатирующего и формирующего.

В ходе поисково-констатирующего эксперимента, в котором приняло участие 168 учащихся 8-10 классов, 89 студентов-математиков и 26 учителей математики, осуществлялась работа по определению возможностей реализации идеи принципа двойственности в школьном курсе математики, разрабатывались содержательные и дидактические основы его использования в качестве не только математического, но и методического принципа, а также методика диагностики готовности учителей и учащихся к его восприятию.

Проведено:
1) исследование удовлетворенности учащихся изучением школьного курса геометрии и степени готовности к восприятию идеи двойственности;
2) анкетирование учителей математики и студентов-математиков после проведения мастер-класса для оценки степени восприятия теоретико-методических идей курса «Двойственные преобразования»;
3) помощь студентам в ходе педагогической практики в организации использования двойственности при построении уроков геометрии;
4) анализ вузовских пособий по методике обучения математике и школьных учебников геометрии с целью выявления возможностей использования идеи двойственности в обучении геометрии.

В результате анкетирования учителей математики и студентов-математиков старших курсов(IV-V<) установлено, что они, будучи знакомы с применением принципа двойственности в проективной геометрии, недостаточно осознают значимость идеи принципа двойственности в математике как науке и даже не предполагают возможностей использования его при обучении математике. Так, в ходе исследования было установлено, что подавляющее большинство (76%) респондентов знакомы с проявлением принципа двойственности в проективной геометрии, но лишь только 11% опрошенных знают о других областях математики, в которых проявляется принцип двойственности, указывая его применение преимущественно в математической логике.

Было также установлено, что высоко оценивая потенциальную возможность применения принципа двойственности при обучении математике и имея желание использовать его в школьной практике, респонденты практически ничего не знают о способах и методике его использования.

Нами также проведен опрос, который позволил выявить отношение учащихся к изучению геометрии в школе. Были измерены индекс мотивации, индекс уверенности в собственных знаниях по геометрии, индекс удовлетворенности процессом изучения геометрии, а также индекс самостоятельности и творческой деятельности. Мы использовали также методику «ассоциаций», предложив учащимся перечислить те прилагательные, с которыми у них ассоциируются личные ощущения и восприятия, связанные с математикой и геометрией. Полученное распределение индексов отражено на диаграмме 1.

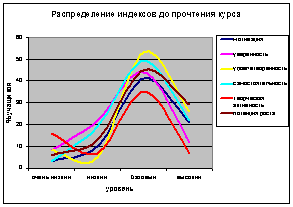
В результате установлено противоречие между достаточно высоким уровнем удовлетворенности уроками геометрии (89%) и низким уровнем мотивации (51%). Кроме того, большинство респондентов отмечают свою неуверенность в знаниях (66%), несостоятельность в самостоятельной (54%) и творческой работе (66%), но высказывают желание исправить сложившееся положение (74%).

Дальнейшая работа велась по отбору содержания и методов обучения. Были разработаны программа, содержание и методика проведения занятий элективного курса «Двойственные преобразования» [8, 9].

В процессе формирующего эксперимента проведено:
а) исследование оценки методических идей курса «Двойственные преобразования» учителями математики и студентами;
б) анализ готовности учащихся к восприятию идей элективного курса «Двойственные преобразования»;
в) разработка и внедрение методической системы обучения курса «Двойственные преобразования» в систему профильной подготовки специализированной математической школы;
г) проверка её эффективности.

Оценка методических идей курса «Двойственные преобразования» учителями математики была получена при:
1) проведении презентации курса на методическом объединении учителей математики г.Ростова-на-Дону;
2) представлении курса на методических конференциях, посвященных специализированному математическому образованию повышенного уровня;
3) участии программы курса в I областном конкурсе программ и методик работы с одаренными детьми;
4) представлении автором курса на Всероссийском конкурсе «Учитель года - 2003» и победе в областном туре конкурса в номинации «Учитель-исследователь». Полученные с помощью эмпирических методов (беседы, наблюдения, интервьюирования) отзывы свидетельствуют о принятии учителями математики идей, заложенных в курсе «Двойственные преобразования» и желании их использования.

Для студентов V курса и магистрантов факультета МИиФ РГПУ (43 чел.) был прочитан спецкурс и проведены мастер-классы, демонстрирующие методику использования принципа двойственности при обучении геометрии в средней школе. Проведенное в конце спецкурса анкетирование позволяет сделать выводы о достаточно высокой степени готовности к использованию этих идей.

Экспериментальная группа состояла из 19 учащихся 8-10 классов, изъявивших желание после презентации курса «Двойственные преобразования» в дальнейшем его посещении. Для оценки эффективности предложенной методической системы мы выделили коэффициент усвоения теоретического и практического содержания курса и пять индексов (мотивации, уверенности использования знания, удовлетворенности занятиями, самостоятельности, творческой активности).  Коэффициент усвоения был измерен по результатам проведенной в конце занятий контрольной работы.

Среднее значение коэффициентов =0,879, величина среднего квадратичного отклонения =0,095, относительная изменчивость =0,108 и показатель точности исследования =0,024, вычислены по результатам проведенного теста.

Полученное среднее значение коэффициента =0,879 свидетельствует о высоком уровне усвоения учащимися учебного материала. Среднее квадратичное отклонение () характеризует разброс значений К_у отдельных учащихся относительно среднего значения по группе. Его значение (0,095) позволяет сделать вывод о том, что К_у отдельных учащихся в основном мало отличаются от среднего значения, а показатель точности исследования (=0,024) подтверждает достоверность результатов.

Соотношение указанных индексов до и после прочтения элективного курса «Двойственные преобразования» представлено на диаграмме 2.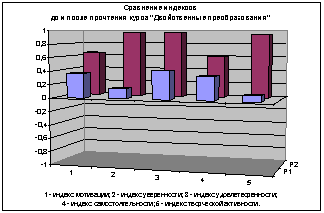

74% учащихся отмечают существенное влияние элективного курса «Двойственные преобразования» на формирование их представлений о математике как о науке познания окружающего мира, отражающей устройство реальной действительности.

Итак, полученные экспериментальные данные позволяют констатировать:

– наличие устойчивой мотивации к изучению курса «Двойственные преобразования» и курса геометрии в целом;

– обеспечение высокого уровня усвоения теоретического материала курса «Двойственные преобразования» и умений использования принципа двойственности при решении различного рода практических задач;

– значительное влияние курса на формирование мировоззренческих представлений учащихся о геометрии и математике вообще;

– положительную динамику роста индексов уверенности, самостоятельности, творческой активности и удовлетворенности учащихся методикой проведения занятий курса.

Все перечисленные факторы говорят о достаточно высокой эффективности курса «Двойственные преобразования», а также об адекватности выбранных нами форм, методов, средств и используемых технологий основным целям и задачам современного математического образования.

В заключении обобщены результаты исследования, изложены его основные выводы, обосновывающие положения, выносимые на защиту, подтверждающие гипотезу, характеризующие достижение основной цели и решение задач исследования; намечены перспективы дальнейшей исследовательской работы.

Основные положения диссертационного исследования отражены в следующих публикациях:

1. Пырков В.Е. Применение принципа двойственности в задачах геометрии построения // Тезисы докладов студенческой научной конференции. Ростов н/Д: Изд-во РГПУ, 1998. С.221-222. – 0,1 п.л.

2. Пырков В.Е. Возможности использования метода двойственности в школьном курсе геометрии // Тезисы докладов студенческой научной конференции. Ростов н/Д: Изд-во РГПУ, 1999. С.135-136. – 0,1 п.л.

3. Полякова Т.С., Пырков В.Е. Учебные пособия для высшей школы Д.Д. Мордухай-Болтовского // Наука и техника: Вопросы истории и теории. Вып. ХVII. – СПб.: Изд-во СПбФ ИИЕТ РАН, 2001. С.77-78. – (0,1/0,05 п.л.)

4.Пырков В.Е., Ханин Е.П. Курсы лекций по математическому анализу, составленные Д.Д. Мордухай-Болтовским // Там же. С.80-81. – (0,1/0,05 п.л.)

5. Пырков В.Е. Анализ Д.Д. Мордухай-Болтовского работы Всероссийских съездов преподавателей математики // Актуальные проблемы подготовки будущего учителя математики. Межвуз. сб. науч. трудов. Вып. 4. – Калуга: Изд-во КГПУ им. К.Э. Циолковского, 2002. С. 131-136. – 0,4 п.л.

6. Пырков В.Е. «Я жил в других мирах …» - о профессоре Д.Д. Мордухай-Болтовском // Гуманитарные и социально-экономические науки. Вып. 1. Ростов н/Д: Изд-во СКНЦВШ, 2002. С.115. – 0,1 п.л.

7. Пырков В.Е. Дмитрий Дмитриевич Мордухай-Болтовской и его методическое наследие // Практические советы учителю: Методический журнал. Вып. 8. Ростов-н/Д: Изд-во РО ИПК и ПРО, 2003. С.32-34. – 0,2 п.л.

8. Пырков В.Е. О возможности применения принципа двойственности в школьном курсе геометрии // Там же. С.34-36. – 0,2 п.л.

9. Пырков В.Е. Факультативный курс «Двойственные преобразования». Программа курса и материалы к проведению занятий // Там же. С.36-47.–1,2 п.л.

10. Полякова Т.С., Пырков В.Е. Тема интеллигенции в публицистике Д.Д. Мордухай-Болтовского 1917-1918 гг// Наука и образование. Известия Южного отделения РАО и РГПУ. Вып. 2. Ростов н/Д: Изд-во РГПУ, 2004. С.142-150. – (0,6/0,3 п.л.)

11. Пырков В.Е. Математика: «Двойственные преобразования в геометрии». Программа предметно-ориентированного элективного курса по предпрофильной подготовке в 8-9 классах / в книге: Гульчевская В.Г. Курсы по выбору в предпрофильном обучении учащихся. Научно-методическое пособие. Ростов -н/Д: Изд-во РО ИПК и ПРО, 2004. С.30-46. – 1,1 п.л.

12. Полякова Т.С., Пырков В.Е. Методическое наследие выдающихся отечественных математиков как источник создания современных методических систем обучения математике // «Математика в современном мире»: Материалы II Российской научно-практической конференции.–Калуга: Изд-во КГПУ, 2004. С.62-70. – (0,5/0,25 п.л.).

e-mail:pyrkovve@yandex.ru